三重県伊勢市桜木町で英語,数学,国語,理科,社会の主要5科目の学力を向上させ 志望する高校へ入学するための水谷塾

　
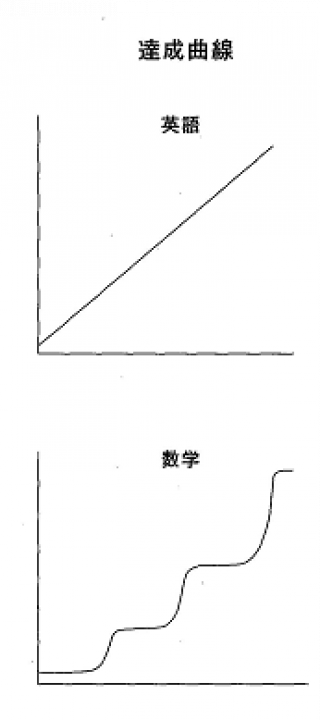
 数学は奥の深い教科です。問題を解くためにはいろいろな能力を必要とします。

　例えば、大学入試センター試験は短い時間の中で教科書のドリル＋αのことをたくさんこなさなければなりません。このような試験に強くなろうと思えば、計算力や作業する力に優れ、素直にいわれるがままの勉強をしてきた生徒が大変有利です。

　問題を見て考えている時間はほとんどありません。自分の頭の中のデータベースに入っている問題から類題を引き出し、組み合わせて、ひたすら速く解くしかないという事です。
    
            
　　　　　センター試験風景

　ところが各国立大学ごとに行われる二次試験は、問題数はせいぜい５題なのに時間は2時間30分ぐらいの時間があります。そこには多少の推理能力や発想力、構想力が必要であり一次試験と違う能力を試していることが多いようです。難関といわれる大学ほどこの傾向が強く、もちろん計算力や作業の速さも必要ではあるのですが、それだけではとても問題は解けません。

　高校入試の試験は、どうでしょうか。県立高校の入試問題は試験時間が45分です。高得点を目指すなら、センター試験と同じく、考えている時間などありません。

　中には推理能力や発想力を試そうとする問題もあったりするのですが、考えている時間がないというのが現実でしょう。

　　　　　　　　
　　　　　　　　過去問はとにかくやらなければなりません。

　式の計算（乗法公式や因数分解など）、平方根、方程式やその利用（利用は読解力がいります。）、関数などはその場で考えるという事ではなく、反射的に手が動くぐらいになっていないといけません。

　今までしつこく述べてきたような、「構造化して記憶する」というようなことは全く関係ないといってよいでしょう。

　数学の本質から考えるとやや忸怩たるものがありますが、そこに私たちのつけ込む要素もあります。

　長年やってきますと、大体これを何度もやればよいといったものが見えてきます。これを時間内に解く練習を繰り返すと、かなりの確率で合格点にまでは達します。

　高得点を目指すなら、図形をイメージする力（図を見ると、合同や相似、等しい辺や角などが見える能力) がいるのですがこれは普段から相当訓練していないと難しいでしょう。この分野だけは誰でも気軽に力がつくという訳にはいきません。

　何年か前、全く宿題をしてこないとんでもない生徒がいましたが、過去問と頻出テーマの演習を塾で繰り返しやっただけで県立の進学校に合格してしまいました。彼は合格が決まって私に報告しに来た際、「家で何もせんと受かってしまった。」と言っていましたが（真似をしてはいけません。運が良かったというだけかも知れません。)このような事は十分あり得る事なのです。

　最後に妙なオチをつけてしまいましたが、数学という科目は本当に厄介な科目ではあります。普段からかなりの集中力と興味を持って勉強しないと毎日やったから成績も比例してアップするというものではありません。

　さて数学の話はこれでおしまいです。また考える事があれば、適宜思った事を書いてみたいと思ってはいますが、ひとまず終了です。

　
平等教育と数学


　現代の数学教育の中心にあるのは、文字式の計算、方程式、関数に、図形の基礎などです。これらの分野の特徴は、ルールを覚え、理解し、簡単なドリルをこなす、といった事を目標とする分野です。


　
　私はあまりよくわからないのですが、もっと試行錯誤や発想力の必要な分野、言い方を変えれば工夫したり、考えたりすることを生徒に学ばせるのに適した分野があるはずです。整数の問題や幾何の問題などそうではないでしょうか。

　思うに戦後の平等教育により、誰でも少し努力すれば機械的にできる計算主体の分野の初歩を教える。そうすれば発想の必要な分野でおこる個人的な学力差は出ません。

　できない子が大量に出るのは平等ではない。という世間の批判をそれでかわそうとする意図があるようです。それでもできない子が出ると、カリキュラムを減らそうということになり、ついに日本の数学の学力は中国や韓国、シンガポール、台湾、香港などの後塵を拝するようになってしまったという事でしょう。
　　　　　　　　
　　　　　　　　発展するシンガポールとマーライオン

　塾を始めてからずっと思っていました。こんな簡単なものでよいのだろうか。落ちこぼれ、落ちこぼれ、とばかり言っているが、わかっている子をもっと伸ばす事は必要ではないのだろうか。

　ひどいときは半数程度の子が、学校の勉強は簡単だから普段はしなくても良い、という事になってしまっていました。



　
　もちろんできない子たちに対する配慮は必要でありますが、できる子たちも、もっと鍛えなくてどうするのだ、という思いは絶えずありました。

　徒競走で、全員が手をつないで同時にゴールするというとんでもない事が話題になりましたが、数学の世界でも全く同じ事が行われていた訳です。
　　　　　　　　　　　

　もちろんゴール前で待っている子たちが、必死にゴールを目指す子たちを応援してあげているのならそれはそれで良い事なのですが、残念ながら待っている子たちは遅い子たちを冷ややかな目で見ている事が多いのです。

　自分は自分でやる事がたくさんあり、余裕もあまりないはずの子たちの方が、後れてくる子たちの面倒を見てあげるのです。

　少しでも勉強をあまいものだと感じてしまうと、人間性に問題のある良くできる子ができあがってしまいます。

　やはり人間は物質面では少し足りない、精神面では自分はまだまだ未熟だ、と思えるような環境にいた方が人間として成長するのではないでしょうか。

　義務教育で同時にこれらの問題（できる子とできない子をどうするか）を解決するのは難しいとは思いますが、できない子たちだけに焦点をあてるのも問題だと思うのです。

　数学という科目がいちばん、できる、できないがはっきりしますので今回このような問題を考えてみました。

　今までは数学という科目の内容を真剣に考えてきたつもりですが、次回実は、高校の入学試験は、数学の本質とは関係ないよ、というような事を言いたいと思います。（じゃ今までは何だったんだと言われそうですが。）

　

今回は数学そのものというより、数学教育について考えたいと思います。

　　野球は小学生の頃から好きで見ていますが、スピードガンが登場しだして間もない頃、巨人のエースだった江川や西本でも140kmそこそこの球速で、結構早いなと思ったものです。今では高校生でもこの程度のスピードを投げる人はざらにいます。ついこの間、夏の高校野球選手権大会の予選で160kmを記録した高校生がいました。
　
　　　　　　　　　　　　
　　　　　　　　　　　　高校時代の江川…この頃が一番速いと言われましたね。　

　　　　　　　　　　　　
　　　　　　　　　　　　西本聖…雑草から這い上がったエース




　無論、昔でも150km台のストレートを投げていた投手もいましたが、明らかに現在のほうが球速の速いピッチャーは多いようです。

　スポーツは現在のレベルが一番高いのではないでしょうか。体操の鉄棒など昔ムーンサルトが初めて登場してから考えても信じられない技で競い合っているではありませんか。
　　
　　　　　　　　　　　　
　　　　　　　　　　　　内村航平の鉄棒…人間業ではないですね。

　教育の世界でも実はかなりの進歩が見られます。数学の本など私が高校生の頃に比べるとものすごく分かり易く、しかもレベルに応じていろいろな種類の参考書や問題集があります。

　またただ単に本を読むというだけではなく、ネットを通じての講義、DVDなども充実しています。わからない点はネット上で質問もできます。

　進歩はいつも、予備校などの激烈な競争にさらされている教育機関から生まれています。競争のないところでは、進歩のスピードは遅いように思われます。皮肉なようですが、大学受験に失敗した生徒たちは真剣に勉強します。その人たちを教える教師は教えることに情熱を注ぎます。応えてくれる人たちがいる訳ですから。

　教えるほうも、教えられるほうも厳しい競争にさらされていますからそこから進化した教え方が生まれるということなのでしょう。

　私などから見ればうらやましくてたまらない現在の教育環境なのですが、生徒の数学力の低下が叫ばれています。

　ゆとり教育が犯人のように言う論調が多いのですが、果たしてそれだけでしょうか。これはつまり教育に関する情報が多すぎて、たとえて言えば食べるものがたくさんあり、どれを食べたらよいかわからない飽食の悩みという側面も無視できません。




　たくさんの食べ物があるから、ちょっと食べてはこれより旨いものがあるのでないかと目移りして、いろいろなものを食べようとします。でもどれも完全に満足するものはない。

　私どものように多少なりとも飢えていた時代ではなさそうです。私が現在をうらやましいと思うほど、生徒たちは現在が恵まれているなどとは思えないのでしょう。

　保護者の方も、どの塾が良いのだろうとか、どの本が良いのだろうとか、熱心な人ほどかけずり回ります。

　＜この先少し「数学に感動する頭を作る」（栗田哲也）から引用します。＞


　中学から高校にかけてやらなければならない数学の量はたかが知れたものです。たくさんの情報を集めて、それで数学ができるようになるというものではありません。



　
　むしろ、数少ない素材をうまく組み合わせる方法を知っている人が数学のできる人なのです。

　ですから、何百という公式や定理を覚えるよりも（つまり情報をたくさん得ることよりも）、少しの公式をどうやって使うか深く考えたほうができるようになるのが数学です。




　
　もちろん数学という学問も日進月歩していますが、こと高校までの教育数学に関する限り、昔のカリキュラムで学んでも、今のカリキュラムで学んでも、大差ありません。　　…引用終わり

　参考書などはこれが自分に合っていると思えば、それをやり抜くことです。また塾なども同じです。信用できると思ったら、とことん信用してください。疑問があったらすぐ相談することです。

　どうもこの国の教育は極端から極端に走るような気がしてなりません。教育そのものは必ず進化しているはずですから、腰を落ち着けて勉強することです。特に数学などの理科系の勉強にはそれが必要です。



　
　実は今回は前回の最後に少し述べた戦後の平等教育と数学について考えるつもりだったのですが、これはまたあとにします。

  　毎日コツコツと勉強すれば、必ず少しずつ学力はついてくる。継続して努力していれば必ずその努力は報われる。というのが勉強に対して普通の人が持つ信仰ですが、数学の場合、そうとばかりは言えないようです。

　うすうす感じてはいましたが、やはりそういうことはあるようです。「数学に感動する頭を作る」（栗田哲也）の本の中での指摘です。下にあげた２つの達成曲線のグラフを見てください。（一部引用）

              

    
                        
                             

    上の２つのグラフは横軸に勉強量、縦軸が達成度（学力）を表しています。
このグラフからわかることは、英語は勉強量と達成度はほぼ比例しています。つまり毎日コツコツ学習すれば、昨日よりは今日、今日よりは明日と着実に学力はつくということです。

　しかし、数学は初めいくら勉強しても、達成度は地を這っています。ところがあるとき学力は急激に伸び始めます。この時期は面白いように学力が伸び、生徒も数学が面白いと感じる時期です。　ところが、しばらくすると、また急に伸びは止まり、再び学力は地を這い始めます。生徒にとっては苦痛なこの時期を何とか乗り切ると、また学力は急に伸び始めます。以下はその繰り返しです。

　これは数学を学習する全ての人に起こる事ではありません。

　同じ事を教えてもすぐ「わかった。わかった。」と言う生徒がいます。実際類題もできるのでわかっているようなのです。
　　　　　　　　　　　　

　
　これに対して、非常に慎重な子もいます。「わかったか。」と聞くと、首を縦には振らないのですが、類題をだすとちゃんと解くのです。
  なんだ、わかっているじゃないかと言うと、「問題は解けてもわかったような気はしない。」と言います。

　この子は、個々の事項は理解したが、その事項と他の事項とのつながりはわかっていない状態、つまり前に言った“理解が構造化されていない”段階でしょう。

　もうおわかりでしょうが、後者の子のほうが、数学が本当によくできるようになる可能性を秘めた子です。彼が納得した後はもう誰も追いつけないほどの伸びを示します。

　ただ問題は、彼は成績が地を這っているとき、その苦しさに耐えかね、自分は頭が悪いのだと真剣に悩んでしまいます。周りの人はどんどん先に行ってしまい、取り残された気になるのです。先生もわかってはくれず、ただ理解の悪いやつだと思われるだけで、彼は一人寂しく数学から離れていくのです。

　私が数学が本当によくできるようになる可能性を秘めた子であったという様なことを申し上げる気は毛頭ないのですが、高校時代に、全く同じ様な経験をしているものですから、この話は非常によくわかるような気がしました。


　高校１年の頃、数学を勉強するたび良く解らないことが出てきた私はよく質問しました。職員室に入って、質問するのは、かなり勇気もいりました。あるとき、定数と変数の区別がイマイチよくできていなかった私はその質問をすると「全然違うじゃないか。」と門前払い的な解答をされたのです。それ以来質問はできなくなってしまいました。



今考えてみれば、確かに全然違うもので、質問するのもどうか、的なのもよくわかるのですが、当時の先生方はティーチングマシーンみたいな人が多く、この問題はこう解く、これはこうだ、みたいなことで、今この生徒がどういう段階か、など考えている余裕はなかったように思われます。

　勉強が続けられるというのは、ある意味精神的な問題なのではないでしょうか。あのとき良く解らないからといって無理矢理結論をつけようとしたり、考えるのをやめてしまうのではなく、わからない事はわからないということで頭の中でその問題を暖めておく、考えることを楽しむ。構造化されていないということで、個々の事柄が全くできない訳ではないので、とにかく次に進む。というような精神状態になっていれば、随分違ったような気がします。

　ただ現在私は中学生を中心として教えている訳ですが、中学ぐらいでは数学の世界は、それほど構造的に複雑ではないように思います。図形のところが厄介ですが、これは構造化した記憶が大切ということよりは、図形をイメージする力が重要でしょう。（詳しくはまた機会があれば書きたいと思います。）何にしろ、数学にはいろいろな能力が必要なようです。

　それともう一つ、戦後の平等教育は数学にもその影響を及ぼしているのですが、その話はまた次回にすることにします。

 今回は、前回「鶴亀算」と「差集め算」が同じに見えない人は同じに見えるまで寝かせておき、解るまで暇さえあれば考えましょう。と言う話をしましたがそもそも数学の問題が解るとはどういうことなのでしょう。

　何年も教えているとこの子は解っているようだが、この子は解っていないな。というのはだいたい区別できます。ただその判別を言葉で言い表したり、説明するのは至難の業です。

　数学の専門家（正確には数学を教えている専門家）がこのような事に言及している書物はないものかとずっと思っていましたが、先日紹介した「数学に感動する頭を作る」（栗田哲也）という本にそのことが書かれていました。

　言葉にはできないが、自分で経験して何となく見えてきているものを、このような専門家や作家の皆さんは実に的確に言葉にして表してくれる事がよくあります。

　一言で言えば、「（数学の問題などが）解る。」とは「ピンとくる」という事です。私も生徒に教えていて、その子がＡ→Ｂになるのは解る。Ｂ→Ｃも解る。じゃＡ→Ｃなのも解るでしょう。と言うと「解るような気もするが、よく解らない。」というような事をそれこそ数限りなく経験してきました。

　どうもそれは「ピンときていない」らしいのです。「ピンとくる。」というのは、栗田氏によると「わかるとは、自分が抱いている世界の中に、きちんと（ピンと）未知事項を位置づける能力」のこと。つまり「ああ、あれと同じことなんだ、いつかやったことのあるあれと同類だ。ちょっとの違いはあるけど大筋はあのイメージだな。」そんな風にして人は理解する、という事です。

　例えば、（分かり易くするためにものすごく簡単な例を使いますが）生徒たちはよく答えが分数にしかならない問題があるとすると、「先生、これおかしい。」と言います。「どこがおかしい。」と聞くと「割り切れへん。」「当たり前だ。分数になるからな。」「あっ、それでもいいんや。」

　これはこの生徒の世界の中には分数がまだ位置づけられていないという事なのでしょう。「各個人が持っている数学の世界」がわかる、わからないを決めてしまうという事です。

　この数学の世界は、絶えず磨いていないと、段々汚れてくるということです。またわかりにくくてごめんなさい。私なりに解釈すると、今習ったことは前に習ったことと、どこが同じなのか、またこれにより前との関連がどうで、どう発展したのかなどを絶えず意識していないと今やっている事がわからなくなる。ということでしょう。
             　　
　　　　　
　　　　　数学のノーベル賞といわれるフィールズ賞メダルです。

 　カミングアウトすれば、私の持っている数学の世界も貧弱なものです。高校の時、ベクトル（前回にも少し言葉は出ましたね。）を習うのですが、「ベクトルって何だ、なんであんなものが要るんだ。」と言われたら…。私の持っている数学世界では何も言えません。

　私の数学世界は高校時代の途中で汚れてしまったのでしょう。前に高校生を教えていた頃、少しベクトルのイメージらしきものが、できかけたような気もするのですが、この子が大学に合格した時点で終わってしまったようです。まして高校時代にはまったくそのようなもののかけらもありませんでした。

　寝かせておくということは、栗田氏の言葉を借りれば「絶えず磨く。」と言うことです。暇さえあれば考えていなければならない。そうでなければ数学のおもしろさは味わえないのかも知れません。

　このように絶えず数学の世界を磨いてきた人は、数学を「構造化して記憶する。」事ができるようになるようです。

また訳がわからないでしょうが、図で説明します。（上記の本からの引用）
　　　　　　　　　

　　　
　上下２つの図を示しましたが、上側のほうの図も下側のほうの図も、大きな四角形は、記憶する頭を表しています。

　上側のほうの人から見ていくと、頭の中には小さな四角、つまり覚えたことがいくつも並列して並んでいます。

　これに対して、下側のほうの人の頭の中には、まず、矢印で示したように、ある事項は別の事項よりも上位概念であるとか、ある事項とある事項は対立概念であるとかいうように、覚えた事柄が、単に並列しているだけでなくて、階層構造をなしていたり、対立概念としての構造をなしていたりします。

　この２つの頭の働きには、雲泥の差があります。

　つまり、上側のほうの人は、数学の問題を解く場合に、何百個もある記憶の四角の中から適切にいくつかの記憶を取り出さなければなりませんが、これは大変なことです。いわばこれは、使えない記憶で、せっかくたくさんのことを覚えても、これらは使えないゴミの山になってしまいます。

　それに対して下側のほうの人は、一つの記憶を取り出したら、それと似た記憶や、対立する記憶を芋づる式にどんどんと取り出すことができます。これは使える記憶で応用が利くのです。（引用終わり）

　解るということ、またそれを極めていくと、構造化して記憶できる頭になることもできそうだ。（普通に毎日コツコツやってればできるというものではなさそうですが。…）ということが少し理解できるような気がしませんか。

ここから派生する数学の勉強はどんなもので、勉強に対するある信仰が数学ではどうも通用しないらしいという事もわかってくるのですがそれはまた次回にします。